末尾Qについて考える - 素数大富豪が8121013倍強くなりたい

はじめに

この記事は「合成数大富豪 Advent Calendar 2024 - Adventar」の17日目の記事になります。昨日は「2,5で割り切れる回数のお話 - 素数大富豪が8121013倍強くなりたい」でした。今日の記事では昨日紹介した5Qチェックをちょっと使います。

今日は末尾Qの数について、２で割り切れる回数と2で割った後の奇数の関係について見ていこうと思います。結構覚えやすい性質があったり、合成数の探索し甲斐もあると思ったので共有しておきます。

合成数をたくさん覚えるにあたって、できるだけ情報量を圧縮しつつ、ど忘れした時に検算できるようにしたいという思いがあります。そのような要請のためには色々な視点で合成数を見ることが大切だと考えています。今回の内容はその足掛けとなるはずです。

末尾Qの数の性質

$nQ= 2^mh$ とする。 $h$ は奇数。( $h$ は必ずしも素数ではない。)

$nQ$ は要するに $100n+12$ のことで、 $4$ の倍数なので $m≧2$ 。

末尾2桁について調べたいので $\bmod100$ で考える。

$2^mh\equiv 12 \bmod100$

$4$ で割って、

$2^{(m-2)}h\equiv 3 \bmod25$

ここで、

$2\cdot 13\equiv 26\equiv 1\bmod25$

なので、*1

両辺に $13^{(m-2)}$ を掛けて、

$2^{(m-2)}h\cdot13^{(m-2)}\equiv 3\cdot13^{(m-2)} \bmod25$

$h\cdot1^{(m-2)}\equiv 3\cdot13^{(m-2)} \bmod25$

$h\equiv 3\cdot13^{(m-2)} \bmod25$

となる。

例えば、 $m=9$ のとき、

$h=3\cdot13^{(9-2)}\equiv3\cdot13\cdot(2197)^2\equiv13\cdot3^3\equiv13\cdot2\equiv1\bmod25$

よって、 $g$ を非負整数として $h=25g+1$ となるが、 $h$ は奇数としたので $h=50g+1$ 。

実際、2^9*51=26AQ、2^9*101=5A7Q、2^9*151=773Q、2^9*251=Q85Qなどとなります。(赤字は最左辺もしくは最右辺なのに素因数分解になっていないことの強調。途中で忘れてたらごめん。)

$m=11$ のとき、前述の結果を用いて、

$h=3\cdot13^{(11-2)}\equiv3\cdot13^{(9-2)}\cdot13^{2}\equiv1*13^2\equiv169\equiv19\bmod25$

$h$ が奇数なことを考慮して $h=50g+19$ 。

2^11*19=389Q、2^11*69=1413Q、2^11*169=346AQ

などが得られます。

なんか大変そう......

上で書いたことは正しいハズですが、実際に $h\equiv 3\cdot13^{(m-2)} \bmod25$ をそのまま暗算で使うのは大変なので実用的な方法を説明します。我々は2^9=5Qを知っているので、これを使いましょう。

$m\le9$ のときは、

$2^{9}\equiv 2^m\cdot2^{9-m}\bmod25$

のように変形して、

$h\equiv 2^{9-m}\bmod25$

とすればよい。

例:

$nQ=2^7h$ となる $h$ を求める。

$2^9\equiv2^7\cdot2^2 \bmod25$

$h\equiv4 \bmod25$ とすればよい。

すなわち、 $h=50g+29$ がわかります。これ便利ですねぇ。

なお、どの $m$ に対しても、 $h=50g+x$ という形になります。

$m\le9$ のときは、具体例も抑えて予め覚えておきましょう。

m=2のときは、Q=2^2*3を考えると、h=50g+3となるので末尾2桁が03,53

m=3のときは、3Q=2^3*39を考えると、h=50g+39となるので末尾2桁が39,89

m=4のときは、AQ=2^4*7を考えると、h=50g+7となるので末尾2桁が07,57

m=5のときは、KQ=2^5*4Aを考えると、h=50g+41となるので末尾2桁が41,91

m=6のときは、2AQ=2^6*33を考えると、h=50g+33となるので末尾2桁が33,83

m=7のときは、37Q=2^7*29を考えると、h=50g+29となるので末尾2桁が29,79

m=8のときは、69Q=2^7*27を考えると、h=50g+27となるので末尾2桁が27,77

m=9のときは、5Q=2^9を考えると、h=50g+1となるので末尾2桁が01,51

などとなります。

$m\ge 10$ に関しては、

$2\cdot 13\equiv 26\equiv 1\bmod25$

という関係を用いて

$2^{(9+r)}\cdot 13^{r}\equiv 2^9\bmod25$

を考えると良さそうです。( $13\equiv2^{-1}\bmod25$ なのでやっていること自体は上と何も変わりませんが、個人的な計算のしやすさ的に分けています)

m=10のときは、2^10*13を考えてh=50g+13となるので末尾2桁が13,63

m=11のときは、2^11*13^2=2^11*169を考えてh=50g+19となるので末尾2桁が19,69

m=12のときは、2^12*13^3=2^12*2197を考えてh=50g+47となるので末尾2桁が47,97

m=13のときは、同様にh=50g+11となるので末尾2桁が11,61

などとできます。mがもっと大きいときは咄嗟に計算するのは厳しいかもですが、需要があれば覚えていきたいですね。未探索ですが、使いやすいものがたくさん眠っているはずです。

ｍが20以上のとき

m=14,......,19のときは飛ばして、mが20以上のときを考えます。

$2$ は $\bmod 25$ の原始根だったりします。

要するに $2^m$ は $m=\phi(25)=20$ のとき初めて $2^m\equiv1 \mod25$ となります。

nishimuraさんのx^k(mod N)のスクリプトを使って2^kを見てみましょう。(原始根合成数とかでググったら出てきてびっくりした)

たしかに2^20で初めて1になってますね。

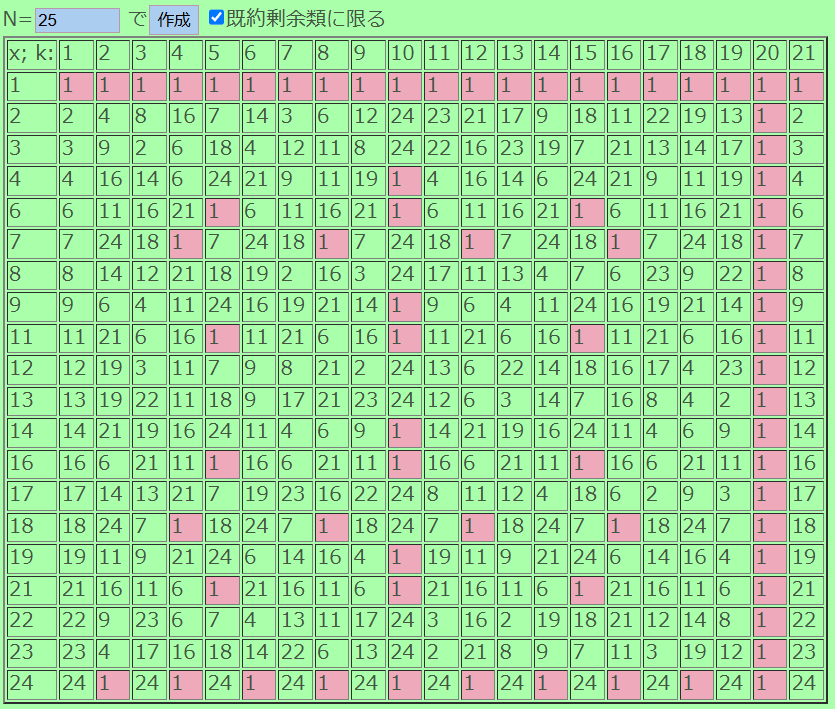
$2^{20}\equiv1$ となることを考えると、2^29の末尾がQになることが計算せずともわかります。(実際2^29=536870912。0あって使いづらいのが残念(´-ω-`))

2^23*n89などのデカい末尾Qを探したりもロマンあって楽しそうですね！！

746586AQ=2^23*89

T8Q9A57Q=2^23*Q89

などなど

実戦での使い方

昨日の記事にて紹介した5Qチェックを用いて2で割れる回数を求めれば、楽に素因数分解ができるケースがあります。全く万能な手法ではありませんが、それなりに役に立ちそうです。

例1:

QAQについて考えます。

$v_2(QAQ)=v_2(11600+512)=v_2(116)+2=4$

よって、QAQ=2^4*n07もしくはQAQ=2^4*n57になります。

ここで、9Q=2^4*3*A9を引くと、

QAQ-9Q=11200=2^4*700となるので、

QAQ=2^4*700+2^4*3*A9=2^4*757

とわかります。AQを引いても良いのですが、2^4*(n*100)となる方が楽なので、9Qを引いています。

もう1つ例を出しましょう。

例2:

J7Qについて考えます。

$v_2(J7Q)=6$

よって、

J7Q=2^6*n33もしくはJ7Q=2^6*n83となります。

ここで、2AQ=2^6*33もしくは53Q=2^6*83を知っていれば、

2AQ=2^6*33を使うと、

J7Q-2AQ=9600=2^6*150

よって、

J7Q=2^6*150+2AQ=2^6*(150+33)=2^6*183=2^6*3*6A

もしくは、53Q=2^6*83を使うと、

J7Q-53Q=6400=2^6*100

よって、

J7Q=2^6*100+53Q=2^6*(100+83)=2^6*183=2^6*3*6A

となります。どちらを使うかは好みですが、結果としては53Qの方が楽に計算できていますね。

また、2AQ=2^6*33や53Q=2^6*83を知らなくとも、J7Q=2^6*n33もしくはJ7Q=2^6*n83と絞り込むだけでもかなりありがたいです。

J7Qは3の倍数かつ、12800=2^6*200よりちょっと小さいので、2^6*183とわかります。(かなりアドホックなテクニックですが......)

オススメの合成数

理論ばっかり語ってもアレなので、実際に末尾Qについて調べたのでオススメを列挙します。今回紹介した性質を使って電卓ポチポチで探したものが多く含まれています。特に、2^m*(素数)となるものは素数の末尾2桁に注目してみてください。上で書いたことが成り立っています。(そうじゃなきゃヤバい)

手打ちなので各自チェックお願いします。(間違っていたら指摘してください。)

83Q=2^3*T39

T3Q=2^3*Q89

J9Q=2^3*A489

5JQ=2^3*6389

6JQ=2^3*7639

AT3Q=2^3*K789(いいお財布)

73Q=2^4*457

89Q=2^4*557

QAQ=2^4*757

K7Q=2^4*857

3KQ=2^4*A9*T3

5KQ=2^4*3*T69

7KQ=2^4*4457

9KQ=2^4*K*439

T97Q=2^4*6857

Q97Q=2^4*J^2*67

6Q9Q=2^4*3*AK^2

77Q=2^5*24A

4KQ=2^5*Q9A

8T9Q=2^5*3*8447

53Q=2^6*83

85Q=2^6*7*A9

J7Q=2^6*3*6A

437Q=2^6*683

TAQ=2^7*79

6KQ=2^7*479

549Q=2^7*3*J*K

9Q5Q=2^7*7Q9

69Q=2^8*3^3

T93Q=2^8*7*6A

Q869Q=2^8*J*457

4Q85Q=2^8*A6Q7

K3Q5Q=2^9*3^5*T7

K3Q=2^T*K

J57Q=2^T*AK

8837Q=2^T*863

Q7T9Q=2^T*Q4K

389Q=2^J*A9

346AQ=2^J*K^2

Q677Q=2^J*6A9

7T45Q=2^J*3469(特にオススメ)

8Q85Q=2^J*3^4*7^2

J6TAQ=2^J*5669

89989Q=2^Q*K^3

4997Q=2^K*6A

66437Q=2^K*8J

なお、4枚以上の末尾KQについては後日、末尾~TKQのときに紹介します。

おわりに

後半で5Qチェックと共に紹介したことは、AQや9Q、2AQなどを使いこなせるようになっていることが前提です。また、私自身出来ていませんが、真価を発揮するためには304=2^4*A9などの普段考えない合成数について、苦手意識を持つことなく素因数分解できるようになることが必要そうです*2。難しそうですね。

誰かこのテクニックを活用してくれないかなぁ、といった感じです。計算早い方だとどれぐらいできるのでしょうか。*3

明日もOTTYで「末尾Q5の探索結果など」です。単に具体的な合成数を列挙する記事になりそう！！！

参考文献など

script

↑nishimuraさんのツール。素数大富豪との直接的な関係はないが使用させて頂きました。

*1: $13$ は $\bmod 25$ における $2$ の逆元なの面白いですね。1枚出し最小素数と最大素数を掛けたら1になるとかいう偶然好き。

*2:304は3KQ-9Qを考えたときなどで出てくる

*3:もしかして普通に割る方が早かったりするのか？